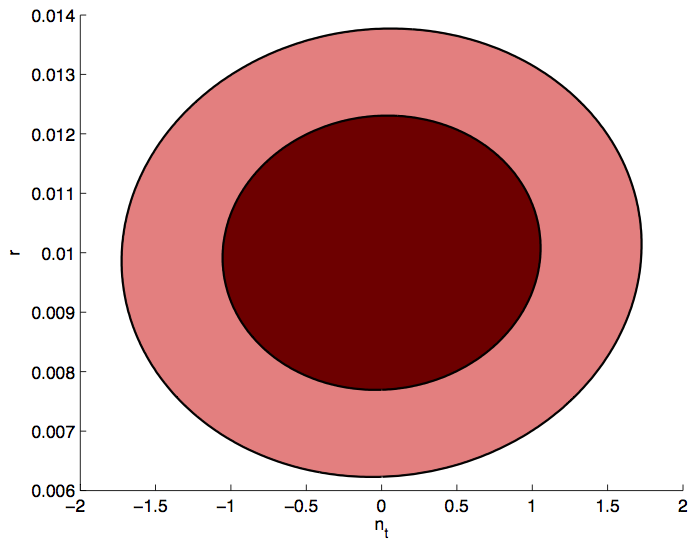
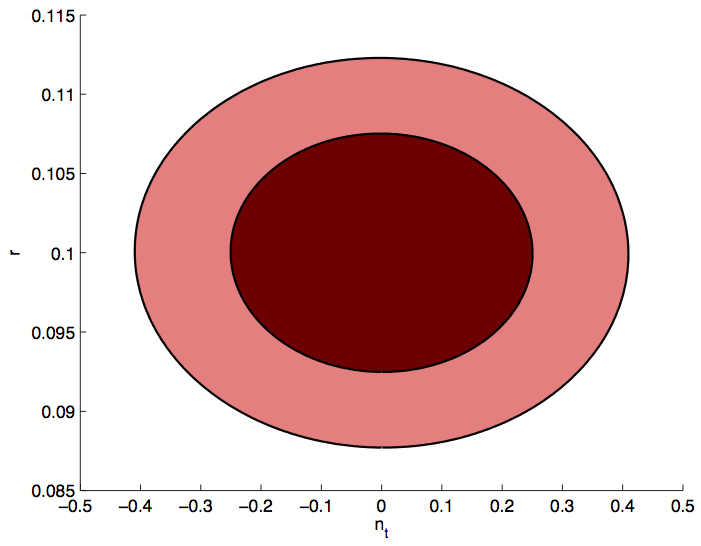
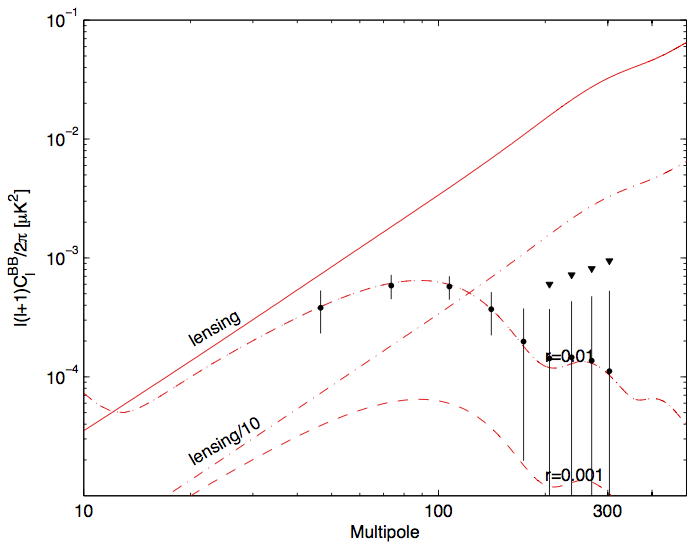
Current: Represent the current state of the \(r-n_s\) plane. These
are the blue contours of Fig7 of BK14 (arxiv:1510.09217); they include Planck TT + lowP + lensing + BAO + JLA + H0 + BK14.
S4+Planck: Represent the projected contours for the combination of
constraints from the small-sky and large-sky portions of the S4, and added
information from Planck.
Given that there is a large dynamic range between the current state, and
the future, I have played around with some plot styles trying to best
capture the improvement we get by going to S4, and leave enough room for
the addition of various theory models. There are three
types of plot: Linear, Linear with a Zoom-In, and Logarithmic.