In 20190220_noiseparams_bk15_forS4 Ben provided \(N_\ell\) fit values extracted from the published BK15 spectra. Using these and the actual BK15 relative hits map I generated sim set 05.00 using the CMB-S4 machinery. I extracted spectra from these in 20190326_bkfinal_05, and Ben then ran ML search on these in 20190410_closedloop_BK15_S4. This closed loop test produced a \(\sigma(r)\) 18% higher than the BK15 result - which I guess can be regarded as a pretty successful cross check.
[We don't expect exact agreement above for at least the following reason: BK15 does scan-wise filtering which removes modes along the \(\ell_y\) axis. This filtering is divided out of the \(N_\ell\)'s producing effective \(1/f\) noise. Upon re-gen this \(1/f\) is included but the filtering is not leading to full mode content but with enhanced noise versus the BK maps. In reality the signal is also filtered so the degree of approximation depends on the signal-to-noise, and will further change as one extrapolates to lower noise regimes. The proper solution would be to remove the modes lost to filtering from both the signal and noise re-gen realizations but one would then need something like the BK "purification matrix" to re-analyze since filtering produces E to B leakage. This would be a massive increase in complexity. Also note that signal and noise are not filtered equally by the scan-synchronous subtraction which is done by BK and other experiments.]
In the past we have scaled the BK bandpower covariance matrix for increases in detector-years, and for changes in sky coverage area, and then converted back to \(N_\ell\) parameters. But it occurs to me that we can instead just multiply and re-deploy the hit map to obtain both of these changes in a very transparent way. We already handled re-deployment of hits this way going from the 04 to the 04b and 04c sim sets.
In this posting I use the expansion from BK15 to S4 bands and scaling by ratio of ideal NET's provided by Ben in 20190829_noise_params_DSR. Specifically I start from the "params.dat" file he provides at the end of that post without the detector-years scaling. I then use the existing machinery to generate sim set 06 using the BK15 relative hits map. The machinery generates full sky noise maps and then divides them by the square-root of the (peak-normalized) BK15 relative hits map to blow up the noise around the edge. The amplitude of the noise in the full sky realizations is tweaked such that when one takes \(N_\ell\) spectra from the post divided maps using the BK15 hit map as apodization mask (i.e. usual inverse variance weighting) one gets back exactly the noise levels specified in the params.dat input file. This means that when re-analyzing these sims one ought to get back the the actual BK15 \(N_\ell\)'s modulo the ratio of ideal NET's scaling (plus a very small additional effect from ignoring the fact that the BK15 \(N_\ell\) bandpowers are mildly correlated). In Section 3 of the 20190829_noise_params_DSR posting Ben quotes the ideal NET numbers he is using - for the record here are the ratios of these:
Band 20 30 40 85 95 145 155 220 270 Ratio 0.744 0.615 0.779 0.939 0.828 0.987 1.057 0.892 1.530
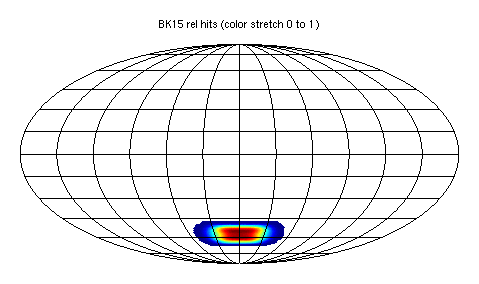
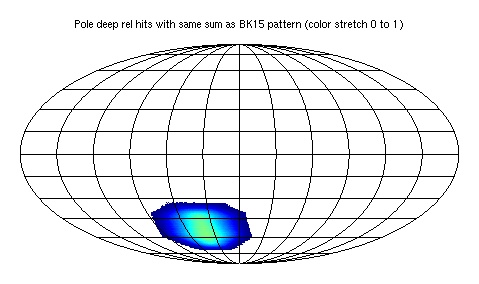
We can then take the full sky 06 noise realizations and generate from them noise maps for any other hit pattern on the sky. I take the "Pole deep" mask provided by Reijo in Deep_SAT_from_the_Pole, scale it to have the same sum as the (peak normalized) BK15 relative hit map, and make it the hit pattern for the 06b sim set. Note that changing the shape of the hit pattern while maintaining its sum corresponds to re-deploying the detector-seconds of integration of the telescope(s) differently for a given amount of observing time. In addition I modify the generator code such that one can provide an optional "reldetyrs.dat" file which specifies the ratio of detector-years to be assumed at each band versus the BK15 base set. Running the generator code again we get the 06b set where the hits have been re-deployed on the sky from BK15 to "Pole deep" pattern, and amplified by the ratio of detector-years going from BK15 to DSR config of S4.
Borrowing again from Ben's 20190829_noise_params_DSR posting:
Note that these ratio numbers are relative to the closest available BK15 band. BK15 has already accumulated a lot of detector years at 150GHz so the S4 145/155 bands will only have 25 times more - the increase will be much bigger at 85/95 and 220/270. At 20GHz S4 will actually have fewer detector-years than BK15 does at 95GHz.
Here are the BK15 relative hits pattern and the "Pole deep" pattern normalized to have the same total hits.
Fig 1:


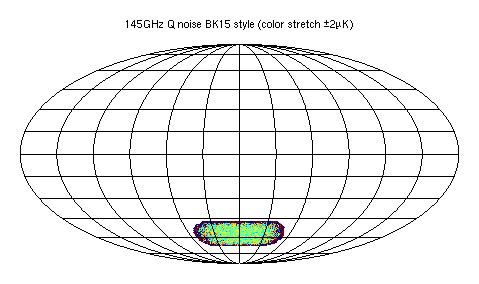
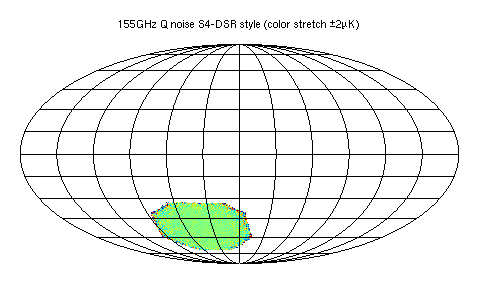
Here are the first Q map noise realizations at 155GHz for these two:
Fig 2:
Here is the full sky noise realization from which the two above were derived. Note that it has similar level to the center of the BK15 plot and much higher than the "Pole deep".
Fig 3:

For the high res delensing bands we could in prinple follow the exact same procedure starting from SPTpol \(N_\ell\) numbers. However, such numbers are not available. The DSR quotes delensing LAT noise level numbers in Table 2-2. These are the "Hi-res Ultra-deep Field" numbers given at this link where it states that these apply for the "Pole deep" pattern and are the noise levels for E/B. I therefore add these high res bands to the 06/params.dat table, take the nside=2048 rhits pattern as the "Pole deep" and run the generator. In 06b/reldetyrs.dat these bands then have unity scaling.
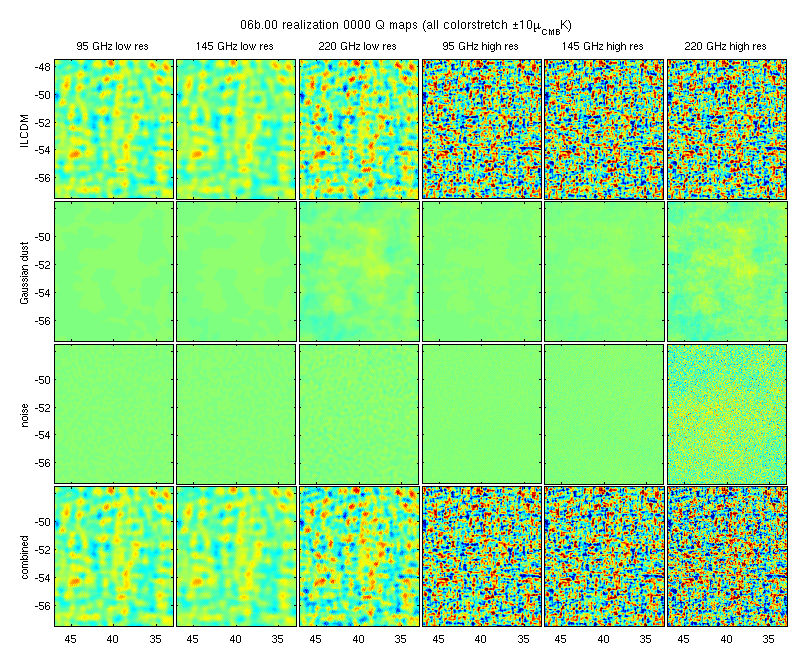
Below are plots similar to the ones in this 2018/2/7 posting showing the low and high res bands for full field and zoom in on central region.
Fig 4: click for zoomable pdf version
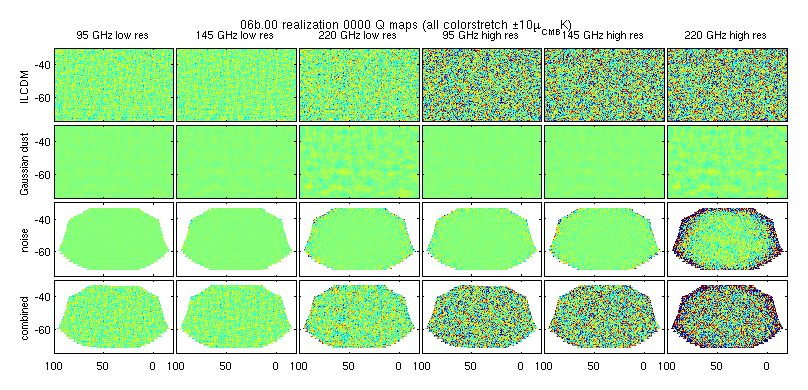
Fig 5: click for zoomable pdf version
For the foreground models we want full sky and high ell for delensing. This limits us to 07 (amplitude modulated Gaussian dust+sync) and 09 (Vansyngel dust+sync). The "amplitude modulated Gaussian" model described in Amplitude_modulated_Gaussian_dust_sims was actually implemented to use the same amplitude scaling across the sky for synch as for dust (contrary to what it says in the posting just linked). The base 00 (simple Gaussian) model will need to be generated since the others borrow the noise realizations from that one.