Recently Reijo posted some scan pattern simulations Pole wide, Chile narrow, and Pole narrow.
In 20190501_obseff I noted that the sum of detector-seconds in the Pole wide and Chile narrow patterns are 0.88 and 0.72 of the nominal calendar year wall-clock time. This is due to some masking of turn-arounds, re-point time between scansets, and, in the case of Chile, non availability of target fields given sun/moon avoidance at certain times of the year.
Let's take a reality check on what efficiency factors look like in the real world for useable scan time per calendar year plus data cut and non-uniform weighting penalties.
I take as an example BICEP3 in 2017 which achieved historically good observing efficiency and focal plane yield - see this B3 SPIE paper for some details. It would be interesting to compare to ACTPol who have shown some impressive observing efficiency in 2015 - see fig 4 here.
During the BICEP/Keck map accumulation process we keep track of the number of pair-seconds binned into each map pixel. Taking the sum over all pixels we get \(7.37 \times 10^9\) pair seconds. The nominal number of light pairs in the focal plane is 1200 so the number above should be compared to \(1200 \times 365 \times 86400 = 3.4 \times 10^{10}\), for a ratio of \(0.195\). This includes inefficiencies from scanning and data cuts.
Each scanset is nominally 50 minutes. From the start of the first scan to the end of the last is 43.4 minutes. After masking out the turnarounds we are left with 33.8 minutes - let's define \(f_\mathrm{scan}=33.8/50=0.676\). In a 3 day observing run there are 73 scansets - \( (73 \times 50)/(3\times 24 \times 60)= 0.845 \) - however, since not all runs are complete and there may be periods when the telescope is broken we won't use this number. Instead let's take the total time spent in scansets used to build the final map verus the calendar year - \( f_\mathrm{year} = (5021 \times 50)/(365\times 24 \times 60) = 0.478 \).
So we expect \( f_\mathrm{year} f_\mathrm{scan} = 0.478 \times 0.676 = 0.323 \) as the fraction of the calendar year getting coadded into the map.
Although the nominal number of light detectors is 2400 only 2012 of these have both halves of the pair marked as nominally functional. Of these a fraction 0.72 of scanset/pair data passes data cuts as shown in this cut plot. So the fraction of nominal which passes cuts is \( f_\mathrm{pass} = (2012\times 0.72) / 2400 = 0.604 \).
So we expect \( f_\mathrm{year} f_\mathrm{scan} f_\mathrm{pass} = 0.478 \times 0.676 \times 0.604 = 0.195 \) as the fraction of nominal detector time over the calendar year getting coadded into the maps - in close agreement with the integration time map.
(The first used scanset was on 2017/03/17 and the last 2017/11/06 which is a 234 day span. For interest we can compare the number of scansets between the first and last days of observing versus the expected number for continuous 3 day runs - \( 5021/((234/3)\times 72) = 0.894 \).)
In the map accumulation process we apply weights to account for the fact that some pairs are noisier than others. We accumulate a weighted integration time map using these which has a total of \(5.29 \times 10^9\) effective pair seconds - a further loss of factor \( f_\mathrm{weights} = 5.29 / 7.37 = 0.718 \) for an overall efficiency versus wall clock nominal of \( f_\mathrm{year} f_\mathrm{scan} f_\mathrm{pass} f_\mathrm{weights} = 0.140 \).
Hopefully CMB-S4 can do a bit better on some of these factors - but we should not assume it it going to do a whole lot better.
Reijo also included in those calcs nominal variance maps using the absolute 95GHz NET's from 20190220_S4_NET_forecasts_III along with the variation versus observing elevation given there. All detectors are assumed to work and to deliver the same idealized NET all the time.
The BK pipeline produces sign-flip noise realizations. Taking the variance over these we can get \(Q\) and \(U\) variance maps. The observing time has been split between these. Noting that: \begin{equation} Q_\mathrm{var}=\frac{\mathrm{NET}^2}{t_Q} \, \mathrm{and} \, U_\mathrm{var}=\frac{\mathrm{NET}^2}{t_U} \end{equation}
we can write \begin{equation} t_\mathrm{obs} = t_Q + t_U = \frac{\mathrm{NET}^2}{Q_\mathrm{var}} + \frac{\mathrm{NET}^2}{U_\mathrm{var}} \end{equation}
and so \begin{equation} \mathrm{NET}^2 = t_\mathrm{obs} \frac{Q_\mathrm{var}+U_\mathrm{var}}{Q_\mathrm{var}U_\mathrm{var}} \end{equation}
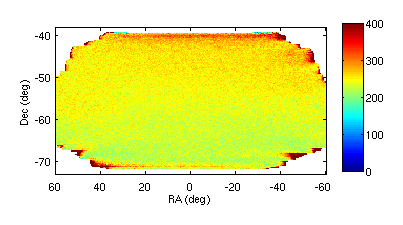
Since the observation time map is in pair seconds the NET we get from this is the pair difference NET. We define pair difference as \((A-B)/2\) so we need to multiply by \(\sqrt{2}\) to go from pair-diff to single detector NET. Below is the resulting map of apparent NET - we see the increase to lower elevation due to increased atmospheric opacity.

Histograming this we get the below.
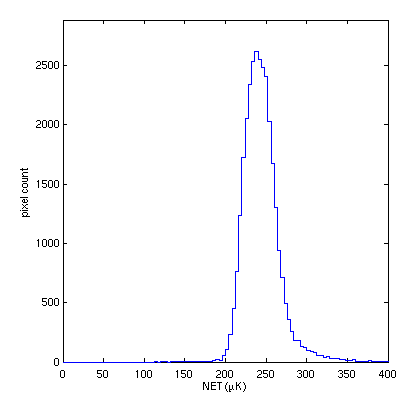
We can compare this to the 262.8 \(\mu\)K\(\sqrt{\mathrm{s}}\) which comes from the model calculation for elevation=56 deg at Pole. Since that it actually higher than the lower half of the histogram here we might claim that we are justified in using the 0.195 number above rather than the 0.140.