CMBS4 Band sensitivity comparison follow-up
Denis and John (2017-02-21)
Summary
Using an independant code, I spot checked the NETs presented in Charlie Hill's Band NET comparison as well as those presented Colin's Tophat bands data challenge. The results here closely match Colin's NET but have significant differences with in Charlie's posting. I strongly suspect the cause for discrepancy is simply due to the different assumptions of instrument loading. The discrepancy would likely be resolved by agreeing upon a common detailed instrument description (physical temperatures and emissivities (or transmittances) of each instrument layer)
I then run a parametric study of NET covering the whole 10 to 300GHz range, 0.1 to 0.5 fractional bandwidth and present the results in this NET pager.
Description
Colin and Victor had calculated NETs for the standard CMB-S4 data challenge 1.0 band definition (as derived from the science book band optimization). These NETs are posted in Colin's Tophat bands data challenge.
Later, Charlie Hill posted a larger matrix of NET calculation using an indpendant code: Band NET comparison on the CMB-S4 wiki.
The goal of this posting is to repeat the NET calculation exercise; to check the assumptions and the results. I do this by modularizing an existing NET calculation code written by John.
The following provides a quick description of how the NET is calculated and what assumptions are made. The final NEP (noise equivalent power in W/Hz^1/2) is calculated as the sum of 5 contributions:
- photon noise = (1) shot + (2) bose noise
- detector noise = (3) phonon + (4) shunt + (5) tes noise
Photon noise
To calculate photon noise (both shot and bose contributions), we estimate the total loading. This done by setting up an instrument as a layered structure in which each layer is defined by its physical temperture, its emissivity \(\epsilon\) (and therefore a transmitance (\(Tx = 1-\epsilon \))). We add two layers on top of the instrument layers for the cmb and the atmosphere.
Here's for example the instrument layers assumed for a Keck-like instrument at 100GHz. For other frequencies, only the emissivities of the windows, filters, and lenses change.
Tx1 = ones(size(atm.Tx))
s(1).name = 'cmb'; s(1).T = 2.73 ;s(1).Tx = Tx1; s(1).eps = Tx1;
s(2).name = 'atm'; s(2).T = 250 ;s(2).Tx = atm.Tx; s(2).eps = 1-atm.Tx;
s(3).name = 'window'; s(3).T = 280 ;s(3).eps = 0.02 .* Tx1;
s(4).name = 'blocker1';s(4).T = 150 ;s(4).eps = 0.01 .* Tx1;
s(5).name = 'blocker2';s(5).T = 70 ;s(5).eps = 0.01 .* Tx1;
s(6).name = 'blocker3';s(6).T = 30 ;s(6).eps = 0.02 .* Tx1;
s(7).name = 'lenses'; s(7).T = 5 ;s(7).eps = 0.15 .* Tx1;
s(8).name = 'antenna'; s(8).T = 0.28 ;s(8).eps = 0.60 .* Tx1;
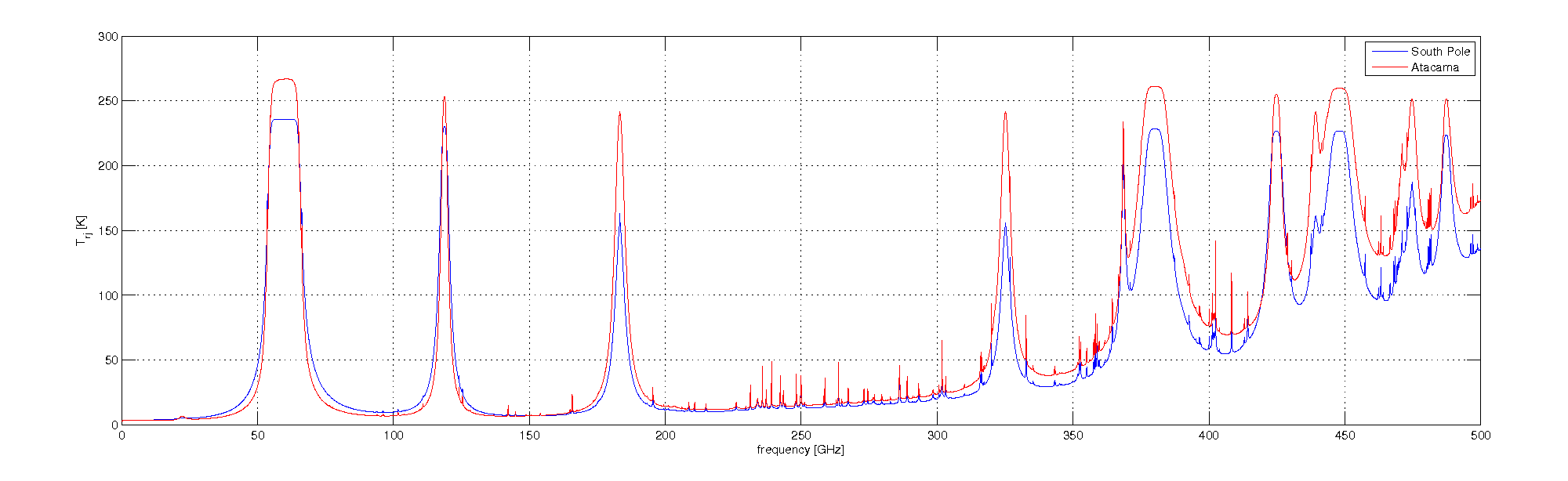
For the atmosphere, we use the brightness temperature and transmittance calculated from Scott Paine's am code. We use the profiles Scott provided us which are the 10-year MERRA2 median profiles. See the profiles (*.amc) and the output spectra ( *.out) for the South Pole, Chajnantor Plateau, Ali observatory in Tibet, and Summit station in Greenland) here. All atmospheric spectra are generated for a zenith angle of 30deg. Here's a view of what the atmospheric brightness temperature looks like for Spole and for Atacama from those profiles.
The instrument definition also includes a band definition (a simple top hat for now), as well as some bolometer parameter definitions.
So compared to Charlie's table of assumptions, the assumptions we make here are very similar:
- band shape: top hat
- PWV: determined by the 10yr MERRA2 median profiles (SP: 425um, CP:931um)
- observation angle: za=30deg (elevation =60deg)
- Optical efficiency: Defined in the instrument layer in the code.
- Telescope loading: Defined in the instrument layer in the code.
- Bath Temp (\(T_0\)): Defined in the instrument layer in the code.
- Transition temp (\(T_c\): \(Tc = 2 * T_0 \)
- Saturation power safety factor: Depends on frequency (2 below 60GHz, 2.5 between 60 and 110GHz, 3 above 110GHz)
- Detector paramters:(\beta\) = 2, \(R_{tes}\) = 0.05, \(R_{shunt}\) = 0.003, \(L_{dc}\) = 20 to calculate NEP_phonon, nep_shunt and NEP_tes.
The optical efficiency, telescope loading and bath temperatures are parameters which can be varied in the code.
Given the above, we run a 1D radiative transfer from the CMB through all the layers all the way to the detector to derive the total loading in Watts on the detectors. The calculation is done assuming the detector is single moded.
The verbose output of the photon noise calculation assuming the South Pole site, at 95GHz (frac_bw = 0.27), bath temp \(T_0\)=0.250K, and a BICEP/Keck-like instrument layers gives:
cmb Tx:1.00, cumulTx to det: 0.31, Power:0.11 [pW], Trj: 1.06 [Krj]
atm Tx:0.96, cumulTx to det: 0.32, Power:1.25 [pW], Trj: 11.54 [Krj]
window Tx:0.98, cumulTx to det: 0.33, Power:0.64 [pW], Trj: 5.93 [Krj]
blocker1 Tx:0.99, cumulTx to det: 0.33, Power:0.17 [pW], Trj: 1.59 [Krj]
blocker2 Tx:0.99, cumulTx to det: 0.33, Power:0.08 [pW], Trj: 0.74 [Krj]
blocker3 Tx:0.98, cumulTx to det: 0.34, Power:0.07 [pW], Trj: 0.62 [Krj]
lenses Tx:0.85, cumulTx to det: 0.40, Power:0.07 [pW], Trj: 0.60 [Krj]
antenna Tx:0.40, cumulTx to det: 1.00, Power:0.04 [pW], Trj: 0.34 [Krj]
Tot Power 2.43 [pW], 22.42 [Krj]
Inst only Power 1.07 [pW], 9.82 [Krj]
The loading above in pW is converted in Krj (referenced to above the atmosphere) by calculating a derivative of the total power (dP/dT) at T=1000K to make sure we are in the Raleigh-Jeans limit. A similar pW to K_cmb conversion factor is also calculated (at T=2.73) to later convert nep into uk_cmb.
Detector noise
The 3 detector noise contributions (NEP_phonon, NEP_shunt, and NEP_tes) are calculated as:
\begin{align}
NEP_{phonon} = \sqrt{4 \; k \;G_c \;T_c^2 \; F^2} \; \; \; \; \; \; \; [W/\sqrt{Hz}]\\
G_c = SF*\frac{Q_{tot}}{T_c} * \frac{1+\beta}{1-(\frac{T_0}{T_c})^{1+\beta}}) \; \; \; \; [W/K] \\
F = \sqrt{1 - D * (\frac{\beta}{2}+1) + D^2*\frac{(\beta+2)*(3\beta+2)}{12}}\\
D = 1 - \frac{T_0}{T_c} \\
\end{align}
\begin{align}
NEP_{shunt} = \sqrt{4 \; k \; T_0 \; R_{shunt} \; (\frac{I_0}{L})^2} \; \; \; \; [W/\sqrt{Hz}]\\\
NEP_{tes} = \sqrt{4 \; k \;T_c \; R_{tes} \; (\frac{I_0}{Ldc})^2} \; \; \; \; \; [W/\sqrt{Hz}]\\\
I_0 = \sqrt{Q_{tot}*\frac{(SF-1)}{R_{shunt}}} \; \; [Amps]\\\
L = \frac{L_{dc}}{L_{dc}-1} \\
\end{align}
see Mather 1982, eq 34 for details
NET
To calculate the complete NET, the 5 contributions of NEP are added in quadrature and converted into NET by dividing by \(\sqrt{2} * dPdT_{cmb}\) calculated earlier.
Results
With this code, I first spot checked of a few cases of Charlie Hill's NET results.
- The first column is just copied from Charlie's table for the nominal CMB-S4 data challenge 1.0 band definition, South Pole, 250mK.
- The 2nd column uses the code presented here and leaves the instrument parameter to default for BICEP/Keck-like instrument loading described above.
- The 3rd column is a copy of the NETs obtained in Colin's originalposting
- The 4th/5th column are the same as the 1st/2nd column with T0 = 100mK.
- The 6th/7th column are the same as the 4th5th with site = Atacama.
- The cases with * are because the band definition used by Charlie differed slightly from the nominal CMB-S4 cases.
| Case: v_cen, frac_bw |
NET_Charlie SP 250mK |
NET BK_loading SP 250mK |
NET_Colin_Victor SP 250mK |
NET_Charlie SP 100mK |
NET BK_loading SP 100mK |
NET_Charlie Atacama 100mK |
NET BK_loading Atacama 100mK |
| 10GHz, 0.33 |
|
311 |
|
|
239 |
|
228 |
| 15GHz, 0.25 |
|
300 |
|
|
235 |
|
221 |
| 20GHz, 0.25 |
|
269 |
|
|
216 |
|
212 |
| 30GHz, 0.3 |
323 |
226 |
244 |
283 |
188 |
268 |
166 |
| 40GHz, 0.3 |
354 |
288 |
306 |
318 |
253 |
278 |
194 |
| 85GHz, 0.24 |
350 |
339 |
346 |
320 |
301 |
280 |
238 |
| 95GHz, 0.24 |
320 |
294 |
295 |
291 |
259 |
264 |
217 |
| 145GHz, 0.22 |
357 |
360 |
350 |
328 |
317 |
322 |
300 |
| 155GHz, 0.22 |
375 |
377 |
368 |
345 |
333 |
350 |
329 |
| 220GHz, 0.22 |
621 * |
813 |
738 |
581 * |
742 |
613 * |
752 |
| 270GHz, 0.22 |
1210 * |
1376 |
1277 |
1143 * |
1270 |
1208 * |
1292 |
We find that:
- In all cases but the highest 2 bands, the resulting NET here matches that calculated in Colin and Victor's original posting.
- In almost all cases but the 145/155 band, we find a discrepancy between the NETs calculated here and those calculated in Charlie's posting. At low frequencies, he find higher NETs. At high frequencies, he find lower NETs, and we have a match only at 145/155GHz bands.
I think the cause for the discrepancy between Charlie's NETs and the ones calculated here is simply the different assumptions for the instrument loading. Since we use the same atmosphere, the loading from the atmosphere is the same. Charlie assumes a constant Trj = 15K instrument loading across all bands, while we let the instrument loading scale by allowing changes in emissivities across the bands. I think this is why Charlie finds higher NETs at his lower frequencies (where our instrument loading is less than 15K) and lower NETs at higher frequencies (where our instrument loading is higher). Even when I try to tweak the instrument definition in the code to get the instrument loading to match his assumed Trj = 15K, I can't quite match Charlie's NETs, supposedly because it depends on the exact contribution of the optical efficiency between the different elements of the instrument.
I therefore suggest that to move forward in obtaining similar predicted NETs, we share a common instrument definition. For exemple, here's the instrument defintion at bands around 100GHz. Only the emissivities of the IR filters, the lenses and the window scale with frequency:
Tx1 = ones(size(atm.Tx));
s(1).name = 'cmb';s(1).T = 2.73 ;s(1).Tx = Tx1; s(1).eps = Tx1;
s(2).name = 'atm';s(2).T = 250 ;s(2).Tx = atm.Tx; s(2).eps = 1-atm.Tx;
s(3).name = 'window';s(3).T = 280 ;s(3).eps = 0.02 .* Tx1;
s(4).name = 'blocker1';s(4).T = 150 ;s(4).eps = 0.01 .* Tx1;
s(5).name = 'blocker2';s(5).T = 70 ;s(5).eps = 0.01 .* Tx1;
s(6).name = 'blocker3';s(6).T = 30 ;s(6).eps = 0.02 .* Tx1;
s(7).name = 'lenses';s(7).T = 5 ;s(7).eps = 0.15 .* Tx1;
s(8).name = 'antenna';s(8).T = bolo.T0 ;s(8).eps = 0.60 .* Tx1;
Parametric study of NET
With this code, I then ran a parametric study of the predicted NET for the multiple bands defined in Charlie's posting. I swept the frequency from 10 to 300GHz in increments of 0.1GHz and the fractional bandwidth from 0.1 to 0.5 and let the code calculate the predicted NET. The only changes to instrument parameters happened at 60, 110 and 183GHz.
- below 60GHz: safety factor = 2.0 and the emissivity of the window and filters was 0.01.
- between 60 and 110GHz: safety factor = 2.5 and the emissivity of the window=0.02 and blocker3=0.02.
- between 110 and 183GHz: safety factor = 3.0 and the emissivity of the window=0.03 and blocker3=0.02.
- above 183GHz: safety factor = 3.0 and emissivity_window =0.04 and emissivity of all blockers = 0.03.
Over the whole [10 to 300GHz] range, this plot shows a contour of NET with center frequency on the x-axis and fractional bandwidth on the y-axis. The obvious breaks at 110 and 183GHz come from the change in instrument definition at those band limits. Also displayed on this plot are the Keck/B3 actual bands for 100, 150 and 220GHz as well as the Buza configuration band definitions. The thick white lines in the 100/150/220GHz bands are the lines for the optimal two non-overlapping tophat bands. These lines trace out the center frequencies of those 2 bands such that they would have equal NETs.

Another way to view these NET forecasts is with this linked NET pager. The pager allows you to toggle between a few different options of site (South Pole vs Chajnantor Plateau), frequency bands (400, 100, 150, 220GHz bands), bath temperatures (100mK vs 250mK) and colorscale (free or fixed [130-100uKsqrt(s)].
